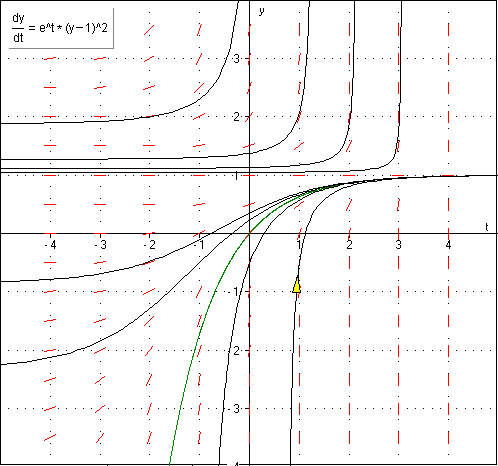
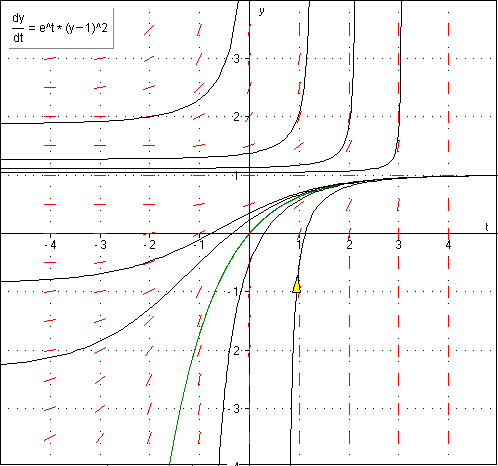
Compreender e classificar as equações diferenciais. O problema de valor inicial. • Resolver equações diferenciais de 1ª. ordem: equações lineares com coeficientes variáveis; equações separáveis; equações exatas e fator integrante. • Compreender as diferenças entre equações lineares e não-lineares. • Compreender os conceitos de equações autônomas e a dinâmica populacional. • Resolver equações diferenciais por aproximações numéricas: método de Euler. • Teorema de existência e unicidade. • Resolver equações lineares de 2ª. ordem ou de ordem mais alta: equações homogêneas a coeficientes constantes; soluções fundamentais das equações lineares homogêneas; independência linear e o Wronskiano; raízes complexas da equação característica; raízes repetidas. • Resolver equações não-homogêneas: método dos coeficientes a determinar; método da variação dos parâmetros. • Compreender a transformada de Laplace: definição e a solução de problemas de valor inicial. • Compreender as aplicações do software Matlab na solução dos problemas de valor inicial.