Workshop on i-Caloric Effects (WiCE 2025)

Register now
From 18th to 19th March Every day from 09h00 to 20h00
Event online The event link has not yet been informed

About the Event

The Workshop on i-Caloric Effects (WiCE) is a biennial scientific event that virtually brings together researchers from a wide range of disciplines to discuss the latest advancements in i-caloric materials and their potential applications. i-Caloric materials are unique in their ability to undergo reversible temperature changes in response to external stimuli, making them promising candidates for energy-efficient refrigeration and heat pump systems.

The 2025 edition marks the fifth occurrence of WiCE. Over the course of two days, leading experts will present their research findings, address the challenges in developing i-caloric materials, and explore various applications across different fields. This workshop serves as a dynamic platform for collaboration and the exchange of ideas, driving progress in this rapidly evolving area of study. By fostering innovation and cooperation, WiCE continues to play a crucial role in advancing the development and application of i-caloric materials, with the potential to revolutionize the energy industry.

Registration to WiCE 2025 that will occur on 18-19 March is open and free of charge through the Doity platform.

The organizers wish all participants a productive and insightful workshop!


Bruno Alho, on behalf of the organizing committee

Follow our social media to keep up with the WiCE news:

Logotipo Instagram Imagens – Download Grátis no FreepikLogotipo do linkedin - ícones de social grátis

Speakers

  • Andrej Kitanovski
  • Anna Kosogor
  • Claudia Masselli
  • Dimitri Benke
  • Edson Passamani Caetano
  • Ekkes Brück
  • Elvina Dilmieva
  • Enric Stern-Taulats
  • Franziska Scheibel
  • Guilherme Peixer
  • João Amaral
  • Johan Cedervall
  • John A. Barclay
  • Juan Bermúdez-García
  • Julie Slaughter
  • Konstantin Skokov
  • Lluís Mañosa
  • Luca Cirillo
  • Michael Maschek
  • Nuno Fortunato
  • Olga Miroshkina
  • Paulo Vinicius Trevizoli
  • R. Nirmala
  • Tino Gottschall
  • Xuefei Miao

Schedule

08h20 - João Amaral Multiscale Approach to Optimized Magnetic Regenerator Geometries Presentation
Place:

Optimizing a magnetic regenerator is a complex multi-physics problem, as both intrinsic thermomagnetic properties of the magnetic refrigerant (magnetization, magnetocaloric effect, specific heat, thermal conductivity) and geometry-dependent effects (demagnetizing field, heat exchange kinetics) play crucial roles. Combining a thermomagnetic model with the Finite Element method allows tackling this optimization problem. We have developed FEMCE - Finite Element Magnetocaloric Effect, a freely available GUI-based simulation tool [1], which we will here present in a user-based perspective.

[1] R. Kiefe and J. S. Amaral, FEMCE (Finite Element Magnetocaloric Effect), available at https://github.com/Rkiefe/FEMCE/

08h50 - Anna Kosogor Landau-Theory Approach to MCE During Magnetoelastic and Magnetostructural Phase Transitions Presentation
Place:

Materials undergoing magnetoelastic and magnetostructural phase transitions hold significant promise for various applications. These transitions involve changes in both the magnetic and elastic subsystems, with the order of the transition governed by the interaction between these subsystems. A special version of Landau-type theory has been developed to quantitatively capture the physical effects accompanying magnetostructural and magnetoelastic phase transitions in multiferroic materials. This approach is based on the analysis of the Gibbs potential, incorporating both magnetic and elastic subsystems and their interplay. This framework allows to describe:

1) the influence of magnetoelastic coupling on the H-T phase diagram during the anisotropic magnetoelastic phase transition in (Mn, Fe)?(P, Si) alloys [1]. It has been shown that the jump in lattice parameters leads to the appearance of hysteresis during the paramagnetic-ferromagnetic phase transition. The magnetoelastic coupling also affects the coordinates of the critical point on the H-T phase diagram, where the first-order phase transition becomes a second-order transition. It’s noteworthy that the interrelation between the critical point and thermal hysteresis has been theoretically predicted for structural phase transitions in Heusler alloys [2] and confirmed experimentally for Fe–Pd alloys [3].

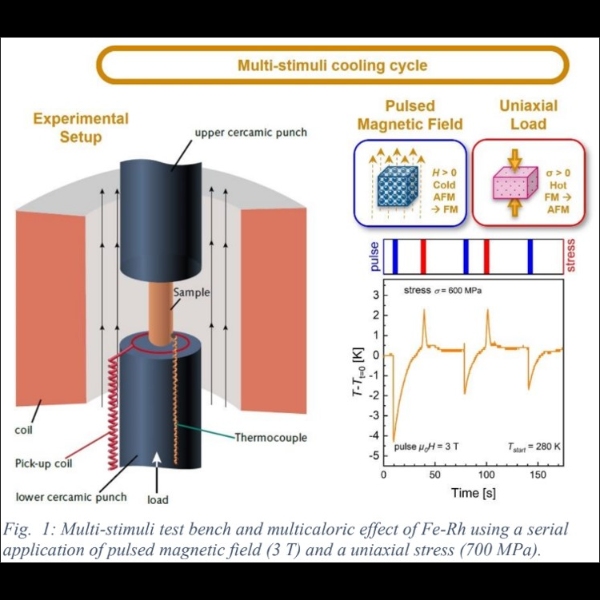
2) the inverse magnetocaloric effect in the Fe-Rh alloy, which undergoes the isotropic magnetoelastic ferromagnetic-antiferromagnetic phase transition [4]. The magnetic-field-induced shift of the phase transition temperature has been calculated and the dependence of the phase transition field on the temperature has been computed. The experimentally observed features of the MCE in the Fe-Rh alloy were explained.

3) the conventional MCE observed during the magnetic Curie transition and giant inverse MCE caused by the magnetostructural phase transition from ferromagnetic austenite to a weakly magnetic martensite [5,6]. It has been shown that the contributions of the elastic and magnetic subsystems to the specific heat are close in magnitude in the temperature range of magnetostructural phase transition.

The Landau-type phenomenological approach bridges macroscopic observations and microscopic models, enhancing the understanding of phase transitions to facilitate the development of novel materials with tailored properties.

[1] Z. Wang, E. Dengina, A. Kosogor, T. Hiroto, X. Tang, N. Kulesh, ... & H. Sepehri-Amin, Materialia, 37, 102195 (2024).

[2] A. Kosogor, N.J. Matsishin, V.A. L’vov, Phase Trans. 86, 796 (2013).

[3] F. Xiao, T. Fukuda, T. Kakeshita, Phil. Mag. 95, 1390 (2015).

[4] V.A. L'vov, A. Kosogor, J. Magn. Magn. Mater. 517, 167269 (2021).

[5] V.A. L'vov, A. Kosogor, J.M. Barandiaran, V.A. Chernenko, J. Appl. Phys. 119, 013902 (2016).

[6] A. Kosogor, J.M. Barandiaran, V.A. L'vov, J.R. Fernandez, V.A. Chernenko, J. Appl. Phys. 121, 183901 (2017).

09h10 - Xuefei Miao Xuefei Miao - Manipulating the magneto-structural coupling in MnCoGe-based magnetocaloric materials Presentation
Place:

Although the magnetocaloric effect (MCE) is intrinsic to all magnetic materials, it is most pronounced (the so-called giant MCE) in those exhibiting a first-order magnetic transition (FOMT) due to the presence of latent heat. In strong contrast to a conventional second-order magnetic transition, the FOMT is characteristic of the coincidence of a magnetic and a structural transition. Therefore, the search for promising magnetocaloric materials can be carried out either by screening the magnetic materials with a naturally coupled magnetic and structural transition, or by tailoring the naturally separated magnetic and structural transitions to coincide.

Stoichiometric MnCoGe alloy undergoes a martensitic transition at 430 K, while its ferromagnetic transition occurs at a much lower temperature of 345 K. Apparently, the magnetic and structural transitions are separated in the stoichiometric MnCoGe alloy. In the present work, we report the realization of a magnetostructural transition and a giant MCE in the off-stoichiometric Mn1-xCo1+xGe alloys. Based on neutron powder diffraction experiments and density functional theory calculations, the mechanism of the tunable magneto-structural coupling in the MnCoGe-based alloys was discussed. Interestingly, the Mn1-xCo1+xGe alloys exhibit a low thermal hysteresis of about 4 K, which is the lowest value reported in the MnCoGe-based alloys so far. Geometrically nonlinear theory has been widely used to explore the relationship between thermal hysteresis and structural compatibility across the martensitic transition in NiTi-based shape memory alloys and NiMn-based Heusler alloys. Based on the neutron diffraction data, we calculated the principal middle eigenvalue λ2 of the transformation stretch tensor for the Mn1-xCo1+xGe alloys. The λ2 was found to be very close to 1, which suggests good structural compatibility between the orthorhombic and hexagonal phase. The structural compatibility at the two phase interface was experimentally verified by high-resolution transmission electron microscope. Furthermore, the giant MCE with thermal hysteresis can tuned in a wide temperature range (from 263 K to 395 K) by doping with appropriate Si. Consequently, the combination of low hysteresis, giant MCE and wide working temperature makes the Mn1-xCo1+x(Ge,Si) alloy promising for room-temperature magnetic refrigeration application.

10h00 - R. Nirmala Magnetocaloric effect in multi-component rare earth intermetallic compounds Presentation
Place:

Study of magnetocaloric effect in rare earth intermetallic compounds is motivated by the occurrence of large magnetic entropy changes that occur near the magnetic phase transitions in these systems that are primarily driven by the order of large moments associated with the 4f electrons of the rare earth. In the present study, compounds with more than two magnetic rare earth elements per a particular crystallographic site are investigated. It is found that such systems show all characteristics of a long-range magnetic order without phase competition. Rare earth intermetallic compounds of type RNi, RNi2 and RAl2 where R site is occupied by a three or more heavy rare-earth elements exhibit significant magnetocaloric properties near the paramagnetic to ferromagnetic ordering temperatures [1, 2, 3, 4].

References

1. Jesla et al, IEEE Transactions on magnetics 59 (2023) 1

2. Jesla et al, Journal of Magnetism and Magnetic Materials 590 (2023) 171651

3. Mohapatra et al, AIP advances 13 (2023) 025011

4. Mohapatra et al, Journal of Magnetism and Magnetic Materials 610 (2024) 17250

10h30 - Michael Maschek Magneto-active magnetic regenerators based on MnFePSi Presentation
Place:

10h50 - Claudia Masselli SUSSTAIN-EL: a rotary elastocaloric heat pump Presentation
Place:

An eco-friendly rotary elastocaloric heat pump is introduced, mainly focusing on the design of the device and of all components. The device mounts 229g of Ni50.8Ti49.2 alloy, shaped as 600 wires (0.5 mm diameter and 30 cm length) and placed inside a circular crown stacked by two concentric cylinders. The airflow meets the wires orthogonally in counterflow to the prototype rotation and a cold and a hot channel are identified. Advanced design solutions to avoid unwanted mixing between the inlet and outlet air currents were adopted. Ten hydraulic pistons (coupled by two to ensure the work recovery) are used for loading the wires.

11h10 - Luca Cirillo Elastocaloric cooling for electronic applications: CHECK TEMPERATURE Presentation
Place:

In recent years, a progressive interest toward elastocaloric cooling, belonging to solid-state technologies based on caloric effects, as promising alternatives to vapor compression technology, has grown. To date, the elastocaloric prototypes developed in the world are about a dozen and they are still far from prospects of commercialization for residential cooling application. Controlling the temperature of electronic equipment is also essential and, currently, there are not elastocaloric devices specifically addressed to this application. In this presentation the CHECK TEMPERATURE project, financed by Department of Industrial Engineering of University of Naples Federico II, is presented: the main purpose of this project is to develop an elastocaloric device targeted on miniature scale for environmentally friendly cooling of electronic components.

13h00 - Konstantin Skokov Dissecting complexity of phase transitions in first-order multi-caloric materials Presentation
Place:

The multi-stimuli responsive functional materials with a strong interplay between their structural, magnetic, and electronic degrees of freedom have been recognized as a new family of promising materials for applications in emerging alternative solid-state refrigeration technologies. In this context, materials with a first-order phase transition, where an application of the different generalized thermodynamic forces/fields is accompanied by large discontinuities and abrupt changes in their conjugate variables are of particular interest. For rational design of these materials, it is vitally important to know in detail, how different subsystems of the solid interplay during the transition, which system triggers the phase transition and how this mutual entanglement interaction can be responsible for the resulting magnetocaloric effect.

Our work shows a new pathway to disentangle the interplay between the structural, magnetic and electronic degrees of freedom, and is the next step towards a complete understanding of the driving forces of the transition, together with comprehension of the origin of thermal hysteresis in magnetic phase-change materials. We have built several original experimental setups for simultaneous measurement of macroscopic physical properties (magnetization, magnetostriction, resistivity, temperature change) in isothermal or adiabatic conditions. These devices were used for study materials with first-order magneto-structural phase transitions, such as La(Fe,Si)13, Heusler alloy, FeRh and RCo2, where the quantitative determination of elastic and magnetoelastic coupling constants is indispensable to understand the nature of field- and stress-driven phase transformation.

13h30 - Olga Miroshkina Electronic structure of all-d-metal Ni(-Co)-Mn-Ti vs. p-d Ni2MnSn: Insights from DFT and XAS Presentation
Place:

All-d-metal Heusler alloys are a new class of caloric materials for energy efficient solid-state cooling. We investigate the peculiar differences of electronic structure between d-d Ni(-Co)-Mn-Ti and p-d Ni2MnSn by combining density functional theory and x-ray absorption spectroscopy (XAS). To retrieve the distinctive characteristics of d-d hybridization in K- and L2,3-edges spectra, we correlate the features in the densities of states and XAS. The comparison of all-d-metal with conventional Heuslers enables us to reveal the impact of a third d-element on magnetic and vibrational properties

13h50 - Johan Cedervall Revealing complex magnetic interactions in Fe2P-based compounds Presentation
Place:

One of the most promising material classes for magnetic refrigeration is (Fe,Mn)2(P,Si), based on the hexagonal compound Fe2P [1,2]. The different atomic positions make it possible to tune the physical properties by chemical substitutions, creating various compositions of (Fe,Mn)2(P,Si) [3]. A systematic study of the impact of Mn substitutions from Fe2P to FeMnP0.5Si0.5 have been undertaken with magnetometry and Mössbauer spectroscopy to understand the magnetic changes that occur during substitution. I will reveal complex magnetic interactions found by small amount of Mn-substitutions.

[1] N. H. Dung, Z. Q. Ou, L. Caron, L. Zhang, D. T. Thanh, G. A. D. Wijs, R. A. D. Groot,

K. H. Buschow, and E. Bück, Advanced Energy Materials 1, 1215 (2011).

[2] L. Lundgren, G. Tarmohamed, O. Beckman, B. Carlsson, and S. Rundqvist, Physica Scripta

17, 39 (1978).

[3] V. Höglin, J. Cedervall, M.S. Andersson, T. Sarkar, M. Hudl, P. Nordblad, Y. Andersson,

M. Sahlberg, RSC Advances 5, 8278 (2015)

14h50 - Lluís Mañosa Caloric properties of spin crossover complexes Presentation
Place:

Spin crossover (SCO) complexes are metallorganic compounds which exhibit a phase transtition from a high-spin to a low-spin states. The SCO transition involves significant changes in magnetization and volume, and it can be triggered by diverse external stimuli such as temperature, pressure and light irradiation.

The sensitivity of the SCO transition to external stimuli and its large latent heat confer significant caloric properties to these complexe. Furthermore, SCO complexes are made of easily available, non-toxic and reciclable elements, which makes them good candidates for environmentally friendly cooling technologies.

In my talk I will report on the magnetocaloric, barocaloric and elastocaloric properties of prototype SCO complexes subjected to the application of magnetic field, hydrostatic pressure and uniaxial stress, respectively. I will show that SCO exhibit giant barocaloric effects but weak magnetocaloric effects. Furthermore, the study of polymer/SCO composite materials has revealed sizeable elastocaloric effects associated with the SCO transition.

15h20 - Nuno Fortunato Computational search of materials with magneto-structural transitions for caloric applications Presentation
Place:

Magnetic refrigeration requires materials with optimal magnetic and structural properties, but no unified design strategy exists to address first-order magnetic transitions in silico. To this end, we implement a DFT-based workflow to screen for magnetic and structural states driving these transitions, while accounting for finite-temperature effects. By using the Curie temperature window and isostructural substitution, we identify MM’X and all-d-metal Heusler compounds with potential magneto-structural transitions [1,2].

[1] N. M. Fortunato et al., Adv. Sci. 36 (2023)

[2] N. M. Fortunato et al., Chem. Mater. 10 (2024).

15h40 - Julie Slaughter Caloric Heat Pump Applications Presentation
Place:

Interest in replacing refrigerants in heating and cooling applications has been accelerating with recent European regulations on PFAS [1] and U.S. and worldwide environmental concerns. Magnetocaloric and elastocaloric technologies promise to be efficient, clean replacements for vapor compression in many applications. Recent progress in systems and applications at Ames National Laboratory will be discussed including advancements in elastocaloric materials and active regenerators, magnetocaloric devices [2] and applications, and new application areas.

Acknowledgements: Magnetocaloric results of this work were performed with joint funding from the Advanced Manufacturing Office and the Building Technologies Office of the Office of Energy Efficiency and Renewable Energy of the United States Department of Energy. Elastocaloric results of this work were performed with funding from the U.S. Department of Defense Strategic Environmental Research and Development Program. Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University of Science and Technology under Contract No. DE-AC02-07CH11358.

[1] Pearson A., What’s All the PFAS About? ASHRAE J 2023;65:120–120.

[2] Slaughter, J., et al., (2025). Scalable and compact magnetocaloric heat pump technology. Applied Energy, 377, 124696. https://doi.org/10.1016/J.APENERGY.2024.124696

13h30 - Dimitri Benke Recent progress on the commercialization of room-temperature magnetic refrigeration Presentation
Place:
We have built “Polaris”, a magnetic beverage cooler in a small series of 60 devices (45 finished as of December 2024). After an initial design and devices built, the design was
adapted to improve the general quality of the device significantly. Additionally, we report on our next device generation “Eclipse” developed in 2024. It was integrated in a double door refrigerator cabinet with a cooling volume of 1000 l. We compare the observed performance with an estimated upper limit of cooling power that a given magnetic refrigerator can potentially achieve, using the approach described in [1].
[1] Dimitri Benke, Maximilian Fries, Tino Gottschall, Dominik Ohmer, Andreas Taubel, Konstantin Skokov, Oliver Gutfleisch; Maximum performance of an active magnetic regenerator. Appl. Phys. Lett. 15 November 2021; 119 (20): 203901.
13h50 - Franziska Scheibel Multicaloric effect, exploiting the thermal hysteresis in a multi-stimuli cycle combining pulsed magnetic field and uniaxial load Presentation
Multicaloric effect, exploiting the thermal hysteresis in a multi-stimuli cycle combining pulsed magnetic field and uniaxial load
Place:

Materials with first-order phase transitions, such as Fe-Rh or Ni-Mn-X (X: In, Sn, Ti) alloys, exhibit large magnetocaloric effects. However, the intrinsic thermal hysteresis in these
materials poses a challenge, limiting reversible transformations in moderate magnetic fields (< 2 T). Several strategies to reduce thermal hysteresis are investigated, often leading to a
reduced caloric effect. Addressing this limitation, the possibility of using multicaloric materials exposed to multiple external stimuli has been investigated. For materials with magneto-
structural or magneto-volume transition, a multi-stimuli approach combining a magnetic field and uniaxial stress can overcome or exploit the thermal hysteresis and realize reversible caloric
effects despite the thermal hysteresis of the first-order phase transition. The two stimuli can be
applied serial or parallel. We developed a multi-stimuli test bench using pulsed magnetic fields up to 9 T and uniaxial loads up to 10kN. The serial exploiting hysteresis multi-stimuli approach facilitates reversible caloric effects and enables pulsed magnetic fields since the serial process uses the magnetic field only for forward transformation. The reverse transformation is induced by the uniaxial load, allowing the decoupling of magnetic field application and the heat transfer processes. First, experiments on a Fe-Rh alloy with a thermal hysteresis of 28 K and a transition width of 30 K show that using a single stimulus of 1.9 T leads to a magnetocaloric effect of -6.7 K, which is entirely irreversible. However, for the combination of the serial application of a 3 T magnetic field and 700 MPa uniaxial stress, a reversible multi-caloric effect of ±2.5 K could be demonstrated despite the large thermal hysteresis (28 K). As the first apparatus of its kind, it opens new avenues for investigating multicaloric effects across various materials, enabling systematic optimization of thermal cycles.

This work is supported by the ERC Adv. Grand CoolInnov, the CRC/TRR 270 HoMMage, BEsT, and the HLD at HZDR (EMFL).

[1] F. Scheibel et al., J. Appl. Phys. accepted for 137,1, (2025).

14h10 - Enric Stern-Taulats Multicaloric effects in P(VDF-TrFe-CTFE) terpolymers Presentation
Place:

Electrocaloric effects are significantly enhanced by downsizing ferroelectric materials and reducing electrode gaps, improving heat transfer and electric field application. While this geometry allows excellent conditions for applying mechanical stresses, multicaloric effects in electrocaloric materials and the potential of polar mechanocaloric materials remain underexplored.

PVDF-based polymers are outstanding organic electrocaloric polymers [1-3]. The electrocaloric effect in P(VDF-TrFE-CTFE) stems from a relaxor-ferroelectric structure [4, 5] exhibited in a matrix of small a-phase crystals and an amorphous component [6]. Giant elastocaloric effects have recently been unveiled in P(VDF-TrFE-CTFE) terpolymers. They are primarily attributed to the amorphous phase in fully stretched samples with loosened molecular chain entanglements [6, 7].

We have studied the synergic potential of combined electric and mechanical stresses with direct characterisation of the multicaloric effects in P(VDF-TrFE-CTFE) terpolymers using thermometry data. Our research aims to enhance the understanding of the physical origins of caloric effects in the terpolymer and set the stage for further exploration and optimisation of multicaloric systems.

[1] A.Torelló, and E. Defay. Adv. Electron. Mater. 8, 2101031 (2022).

[2] B. Neese, et al., Science 321, 821 (2008).

[3] A, Aravindhan, et al., J. Materiomics 9, 256-260 (2023).

[4] L. Yang, et al. Macromolecules 47, 8119– 8125 (2014).

[5] L. Yang, et al., Polymer 54, 1709-1728 (2013).

[6] Q. Liu, C. Richard, and J.-F. Capsal, Eur. Polym. J. 91 46–60 (2017).

[7] B. Yoshida, et al., Appl. Phys. Lett. 108, 242904 (2016).

14h50 - Ekkes Brück Materials for efficient conversion of low temperature waste heat Presentation
Place:

The production and use of energy account for more than 75% of the EU’s greenhouse gas emissions. Decarbonising the EU’s energy system is therefore critical to reach our 2030 climate objectives and the EU’s long-term strategy of achieving carbon neutrality by 2050. At the same time, we will generate vast amounts of low-grade heat in e.g. datacenters, food, pulp and paper industries that is available 24/7. Efficient machines or devices to convert this low-grade heat in an economically sound way are however lacking. Upgrading only a small percentage, as dictated by laws of thermodynamics, of this otherwise wasted heat into electricity, can already be significant due to the sheer amount of heat in the temperature range below 390 K. As the heat is available and often needs to be downgraded before it can be safely released into the environment, we have similar to PV and offshore wind mainly to consider the cost of investment to determine the economic framework of such a generator. The existing prototypes [1, 2] are essentially proofs of principle but have demonstrated where we can gain efficiency by improving designs and by tailoring materials properties. Promissing materials have to fulfill a few requirements [3]: Low and adjustable Curie temperature for low-grade heat, low remnant magnetization (Mr), which is generally fulfilled as one operates near or at the critical temperature. Significant and steep magnetization change at the Curie temperature as the figure of merrit of this type of materials is proportional to the change in magnetization, and inversly proportional to the heat input required to induce this change in magnetization. A high thermal conductivity to facilitate a rapid temperature change, and last but not least low-costs, which implies the preferred use of earth-abundant elements. A few of these materials requirements are very similar to the requirements for magnetocaloric materials. However, e.g. latent heat that helps for magnetocaloric applications is detrimental to thermomagnetic applications, as it implies more heat is needed to induce a change in temperature. We will discuss current state of the art devices and review developments in tailoring the performance of novel magnetic materials for efficient energy conversion.

Keywords: Energy conversion, magnetic materials, thermomagnetic devices, energy efficiency

References:

[1] T. Christiaanse, E. Brück, Met. Mat Trans. E 1, 36-40 (2014)

[2] A. Waske, D. Dzekan, K Sellschopp, D. Berger, A. Stork, K. Nielsch, S. Fähler, Nat. Energy 4, 68-74 (2019).

[3] D. Dzekan, A. Waske, K. Nielsch, S. Fähler, APL Materials 9, 011105 (2021)

15h40 - Elvina Dilmieva Impact of structural subsystem evolution on the magnetocaloric effect in Heusler alloys Presentation
Place:

In Heusler alloys with a magnetostructural transition the lattice entropy change is one of the dominant contributions along with the magnetic one. However, the hysteresis accompanying the 1st order transition causes efficiency losses in the cyclic cooling process. The study of the structural subsystem is challenging as it requires structural methods in combination with high magnetic fields. Therefore, we present in-situ results on the magneto-induced structural evolution of a Ni-Mn-Ga-Cu alloy and its influence on the magnetocaloric effect, investigated using a developed optical method under high magnetic fields.

16h00 - Juan Bermúdez-García Hybrid organic-inorganic thermomaterials for low-pressure barocaloricc refrigeration and cold-storage applications Presentation
Place:

In the search for more efficient and low-energy consuming barocaloric materials, hybrid organic-inorganic compounds arised as an emerging alternative for low-pressure barocaloric technologies, even offering a dual application for passive cold-storage without energy consumption.[1,2]

In this presentation, we compiled the recent advances of our research group to develop new soft barocaloric and cold-storage materials,[1] from dense ionic plastic crystals[2] and hybrid perovskites[3] to porous metal-organic frameworks[4,5] towards future energy efficient refrigeration technologies.

[1] J. M. Bermudez-Garcia et al., Barocaloric Effects in the Solid State, Book Ch. 6, Ed. IOP, 2023.

[2] J. García-Ben et al., J. Mater. Chem. A, 2023, 11, 22232.

[4] J. M. Bermudez-Garcia et al., Nat. Commun., 2017, 8, 15715.

[5] J. García-Ben et al., Chem. Mater. 2022, 34, 3323.

16h40 - Andrej Kitanovski Challenges, Opportunities, and Future Roadmap for Energy Applications of Magnetocaloric Materials Presentation
Place:

Approximately fifty percent of global final energy consumption is attributed to heating and cooling applications. Additionally, an estimated fifty percent of the total energy consumed globally is lost as unused waste heat. For the purpose of global decarbonization, these two energy sectors - heating/cooling and waste heat recovery - represent a far greater potential for impact than can be achieved through the complete decarbonization of the global transportation sector alone. The demand for energy-efficient and environmentally friendly systems for cooling, heat pumping, air conditioning, and thermal energy harvesting is more pressing than ever. Magnetocaloric and thermomagnetic energy conversion technologies are among the most promising alternatives for achieving these objectives and have been the focus of significant basic and applied research in recent decades. This contribution offers a thorough and current critical review of the advancements and challenges related to the energy applications of magnetocaloric and thermomagnetic materials. It explores potential solutions, as well as overlooked research areas and associated activities. Furthermore, the presentation outlines a roadmap that could facilitate future progress in magnetocalorics and thermomagnetics, emphasizing their viable market applications across various sectors.

17h00 - Edson Passamani Caetano Atomic disorder affecting magnetocaloric properties of Ni2Mn-based Heusler alloys: a study by 57Fe Mössbauer spectroscopy Presentation
Place:

Researchers are still searching for cheaper, safer, chemically/physically stable, and low field magnetic solid refrigerants. In this regard, solids that exhibit structural and magnetic transition temperatures (e.g., some Heusler-type alloys - HAs) closely related to each other may be suitable for application in magnetic refrigeration cycles due to their relatively high magnetocaloric (MC) properties. However, HAs are, in general, highly fragile and have large thermal magnetic hysteresis associated with the structural phase transition, which is highly dependent on the chemical order of the L2?-type structure. Therefore, the proper use of the HAs as solid refrigerants still requires a more extensive study. Since the atomic order is a crucial factor to be better understood, 57Fe Mössbauer Spectroscopy (MS) analysis, which furnishes hyperfine interaction parameters, is a promising experimental technique that may provide new insights into the magneto-structural properties of solid refrigerant materials, such as 57Fe-doped Ni?MnZ (Z = Sn, Ga) Heusler alloys. In this talk, we will explore the role of atomic ordering of the L21-type structure (as observed by 57Fe MS) that determines the MC properties of 57Fe-doped Ni2Mn1.44Sn0.56 Pseudo-Heusler alloy. We will examine a specific case that relates to the influence of grain refinement induced by milling on chemical disorder to simulate the degradation of the magneto-structural transition that may occur during the magneto-thermal operation cycle in these brittle materials.

17h20 - Guilherme Peixer Assessment of Thermodynamic Progression in the Performance of a Large-Scale Magnetic Refrigeration System Presentation
Place:

For a century, vapor compression has dominated refrigeration but faces environmental and regulatory challenges due to refrigerant fluids. This has spurred efforts to improve efficiency and reduce emissions. Magnetic refrigeration, using solid-state refrigerants, offers promise by eliminating harmful gases and enhancing efficiency, though it remains in development. This study examines the evolution of a magnetocaloric air-conditioning prototype across three stages, highlighting design changes, performance comparisons, and future prospects.

17h40 - John A. Barclay Efficient active magnetic regenerative liquefaction for hydrogen and other cryogens Presentation
Place:

Broad use of hydrogen and methane as fuels and energy carriers will provide better energy security, return major economic, environmental, and health benefits, and help minimize the climate change impact of greenhouse gas emissions. Liquid hydrogen (LH2) and liquid natural gas (LNG) are required to store, transport, and use these gaseous fuels for heavy-duty vehicles such as class 7/8 trucks, transit buses, marine vessels, trains, and airplanes because of their relatively higher volumetric energy density and gravimetric energy density compared to compressed gaseous storage. Cost-effective, highly efficient liquefaction of LH2, LNG, and other cryogens is a challenging technical barrier that must be overcome to help establish reliable, sustainable, and affordable cryogenic fuels. Active magnetic regenerative liquefaction is one of the few technologies identified with the potential to achieve much higher efficiency and lower capital costs than conventional gas-cycle liquefaction methods at metric tons/day scale. During this short seminar, I will give sufficient background on active magnetic regenerative liquefiers to illustrate this unique potential.

Carregando área de inscrição

Organizer

WiCE 2025 Organizing Committee

Organizing Committee:
Alexandre M. G. Carvalho
Bruno de Pinho Alho
Paula O. Ribeiro Alho
Paulo Vinícius Trevizoli
Vivian M. Andrade

Scientific Committee:
Érik Usuda
João Horta Belo
Luana Caron
Rodrigo S. de Oliveira
Contact us
Doity The most complete tool for your event.
Create Your Event Right Now
About doity
Events in
Participant Area
Rua José Pontes de Magalhães, 70 Jatiúca, Maceió - AL Empresarial JTR, Ed. Ítalia, Sala 702
see on map

We use cookies on our website to improve performance and experience. By continuing to browse, you agree to the use of such technologies and to our cookies policy .

Next